Questions On Binary Search Tree
All of the below solutions is in continuation of the Binary search Tree program which is written with this post therefore I am not passing root to every method, it is referred from the BinarySeachTree class.
Problem 1: Write a program to print the nodes by levels.
For example in below tree it should print – 6,4,9,2,5,7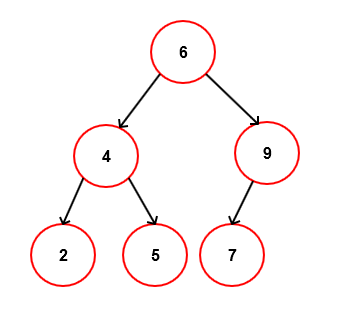
This is nothing but the Breadth First search. You will have to use a Queue to track the nodes.
public void levelOrderTraversal() {
Queue<Node> queue = new LinkedList<>();
Node currNode = root;
queue.add(currNode);
while (!queue.isEmpty()) {
currNode = queue.poll();
System.out.print(currNode.value);
if (null != currNode.left) {
queue.add(currNode.left);
}
if (null != currNode.right) {
queue.add(currNode.right);
}
}
System.out.println();
}
Problem 2: Write a program to check whether a tree is Binary Search Tree or not.
You just traverse node by node and check for the Binary Search Tree conditions.
public boolean isBST(Node root) {
Node curr = root;
Stack<Node> stack = new Stack<>();
stack.push(curr);
while (!stack.isEmpty()) {
Node node = stack.pop();
if (node.left != null) {
if (node.value > node.left.value) {
stack.push(node.left);
} else {
return false;
}
}
if (node.right != null) {
if (node.value < node.right.value) {
stack.push(node.right);
} else {
return false;
}
}
}
return true;
}
Problem 3: Write a program to Find lowest common ancestor of two nodes.
For example in below tree – the lowest common ancestor for 2 and 5 will be 4, the lowest common ancestor for 4 and 7 will 6.
public Node findLowestCommonAccestor(Node child1, Node child2) {
if (root == null || child1 == null || child2 == null) {
return null;
}
while (root != null) {
int value = root.value;
if (value > child1.value && value > child2.value) {
root = root.left;
} else if (value < child1.value && value < child2.value) {
root = root.right;
} else {
return root;
}
}
return null; // only if empty tree
}
Problem 4: Write a program to compute the size of a Binary Search Tree.
We can easily define it recursively. It will be the sizeOf(left tree) + sizeOf(right tree) + 1 (root).
public int sizeOfBinaryTree(Node root) {
if (root == null) {
return 0;
} else {
return (sizeOfBinaryTree(root.left) + 1 + sizeOfBinaryTree(root.right));
}
}
Problem 5: Write a program to find largest Binary Search Tree in a tree.
public int largestBST(Node root) {
if (isBST(root))
return sizeOfBinaryTree(root);
else
return Math.max(largestBST(root.left), largestBST(root.right));
}
Problem 5: Write a program to create mirror image of a Binary Search Tree.
public Node mirrorOfBinaryTree(Node root) {
Node temp = null;
if (root != null) {
mirrorOfBinaryTree(root.left);
mirrorOfBinaryTree(root.right);
temp = root.left;
root.left = root.right;
root.right = temp;
}
return root;
}
Problem 6: Write a program to check whether a BST is mirror image of other BST.
public boolean isMirror(Node root1, Node root2) {
if (root1 == null && root2 == null) {
return true;
}
if (root1 == null || root2 == null) {
return false;
}
if (root1.value != root2.value) {
return false;
} else {
return isMirror(root1.left, root2.right) && isMirror(root1.right, root2.left);
}
}
Problem 7: Write a program to find the height of a Binary Search Tree.
public int findHeight() {
Queue<Node> queue = new LinkedList<>();
Node currNode = root;
int level = 0;
if (currNode == null) {
return -1;
}
queue.add(currNode);
queue.add(null);
while (!queue.isEmpty()) {
currNode = queue.poll();
if (currNode != null) {
if (currNode.left != null) {
queue.add(currNode.left);
}
if (currNode.right != null) {
queue.add(currNode.right);
}
} else {
if (!queue.isEmpty()) {
queue.add(null);
level++;
}
}
}
return level;
}
References
Design and Analysis of Algorithm – Anany Levitin
Beginning Algorithm – Simon Harris, James Ross
Data Structures And Algorithms In Java- Robert Lafore
Introduction_to_algorithms- Corman
