Traversal of Binary tree
Traversing a tree means visiting each and every node in some specified order. Traversing a binary tree is not very common because it is not too fast but it is very useful in some circumstances like finding height of binary tree, size of binary tree etc.
There are three ways to traverse a tree –
Inorder Traversal: An inorder traversal of binary search tree visits all the nodes in ascending order based on their node value. This is very useful if you want to create a sorted list out of binary search tree. To understand it better think like inorder means parent will be in between of left and right child.
There are two ways to perform inorder traversal – recursively and iteratively
Recursive approach:
we start with the root node
- Call itself to traverse the node left subtree
- Visit the node itself
- Call itself to traverse the node right subtree
Iterative approach:
we start with the minimum value node in the tree and visit it and then each successor node until there are no more node remaining. We generally use Stack data structure to keep track of the nodes.
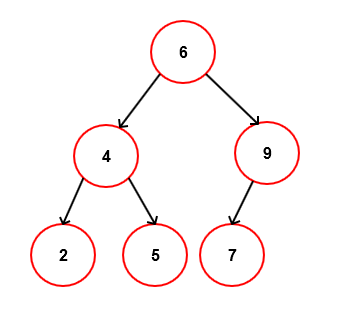
For example consider below Binary Search Tree.
The Inorder traversal will be – 2,4,5,6,7,9
Java implementation of InOrder traversal (Recursive)
public void inOrderTranversalOfTree(Node node) {
if (node != null) {
inOrderTranversalOfTree(node.left);
System.out.println(node.value);
inOrderTranversalOfTree(node.right);
}
}
Java implementation of InOrder traversal (Non-Recursive)
public void inOrderTraversalOfTree() {
Stack<Node> stack = new Stack<>();
Node currNode = root;
while (true) {
while (currNode != null) {
stack.push(currNode);
currNode = currNode.left;
}
if (stack.isEmpty())
break;
currNode = stack.pop();
System.out.print(currNode.value + " ");
currNode = currNode.right;
}
System.out.println();
}
Preorder Traversal: An preorder traversal of binary search tree first visits the root then the left subtree and then right subtree . To understand it better think like preorder means parent will be at the start then left and then right child.
There are two ways to perform preorder traversal – recursively and iteratively
Recursive approach:
we start with the root node
- Visit the node itself
- Call itself to traverse the node left subtree
- Call itself to traverse the node right subtree
Iterative approach:
To achieve preordering of nodes parent-left-right We generally use Stack data structure.
For example consider below Binary Search Tree.
The Preorder traversal will be – 6,4,2,5,9,7
Java implementation of PreOrder traversal (Recursive)
public void preOrderTranversalOfTree(Node node) {
if (node != null) {
System.out.println(node.value);
preOrderTranversalOfTree(node.left);
preOrderTranversalOfTree(node.right);
}
}
Java implementation of PreOrder traversal (Non-Recursive)
public void preOrderTraversalOfTree() {
Stack<Node> stack = new Stack<>();
Node currNode = root;
stack.push(currNode);
while (!stack.isEmpty()) {
Node node = stack.pop();
if (null == node) {
break;
}
System.out.print(node.value + " ");
if (null != node.right)
stack.push(node.right);
if (null != node.left)
stack.push(node.left);
}
System.out.println();
}
Postorder Traversal: An postorder traversal of binary search tree visits the left subtree then right subtree and then the root. To understand it better think like postorder means parent will be at the last i.e. left child-> right child -> Parent.
There are two ways to perform postorder traversal – recursively and iteratively
Recursive approach:
we start with the root node
- Call itself to traverse the node left subtree
- Call itself to traverse the node right subtree
- Visit the node itself
Iterative approach:
To achieve postordering of nodes left-right-parent We generally use Stack data structure.
For example consider below Binary Search Tree.
The Postorder traversal will be – 2,5,4,7,9,6
Java implementation of PostOrder traversal (Recursive)
public void postOrderTranversalOfTree(Node node) {
if (node != null) {
postOrderTranversalOfTree(node.left);
postOrderTranversalOfTree(node.right);
System.out.println(node.value);
}
}
Java implementation of PostOrder traversal (Non-Recursive)
public void postOrderTraversalOfTree() {
Stack<Node> stack = new Stack<>();
Node currNode = root;
stack.push(currNode);
Node prev = null;
while (!stack.isEmpty()) {
currNode = stack.peek();
//go down to the tree
if (prev == null || prev.left == currNode || prev.right == currNode) {
if (currNode.left != null)
stack.push(currNode.left);
else if (currNode.right != null)
stack.push(currNode.right);
else {
//leaf node
System.out.print(currNode.value + " ");
stack.pop();
}
}
//going up to the tree
if (currNode.left == prev) {
if (currNode.right != null)
stack.push(currNode.right);
else {
System.out.print(currNode.value + " ");
stack.pop();
}
}
//moving up from right
if (currNode.right == prev) {
System.out.print(currNode.value + " ");
stack.pop();
}
prev = currNode;
}
System.out.println();
}
Go to the next page – Click on the below red circle with page number.