Deleting a Node
Deletion is little complicated as compared to insertion and search that’s why I kept it at the last. Delete is bit complicated because when you delete a node you will have to consider one of the following condition:-

1. 1. No children: The deleted node is the leaf node means it doesn’t have any children. In this case you can simply remove it.
   2. One children :

The deleted node has one children (left or right). In this case you replace the deleted node with its child.

1. 1. Two children: :

In this case you replace the deleted node with its successor and point right and left subtree of deleted node to the successsor.

CASE-1: Deleting a Node with no children (leaf node)
This is the simplest case of deletion in Binary Search Tree. You will have to just point the deleted node parent to null.
For example suppose that we want to delete 7 from below tree. We will have to just point the node 9 to null.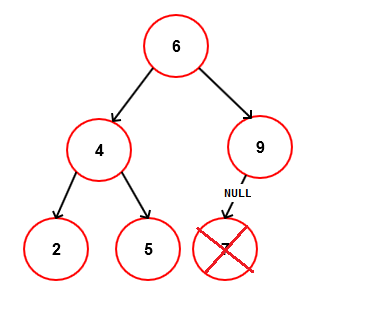

CASE-2: Deleting a Node with one children
This is also very simple. You will have to just point the deleted node parent to the child of deleted node.
For example suppose that we want to delete 9 from below tree. We will have to just point the node 6 (parent of node 9) right child to the node 7 (only child of node 9).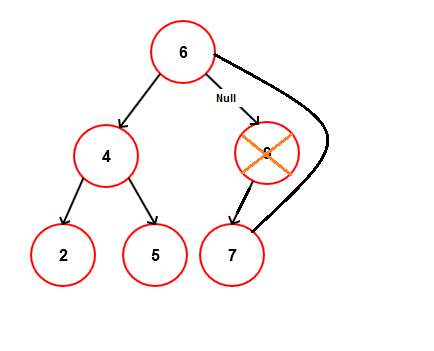

CASE-3: Deleting a Node with two children
Deleting a node with two children is bit trickier than the other cases. Suppose that you want to delete root node 6 from the below tree. The problem is that which node you will put at the place of 6 after deletion. Although we can replace it with its right or left child to maintain BST property but its both the child have their children which makes it difficult to replace with.
Therefore to delete a node (6) with two children, we first find the successor(7) of node (6) which will ofcourse on the right side of the tree- then replace the node (6) with its successor (7). The original right and left subtree of deleted node(6) will now the become the right and left subtree of node(7). If there is any right node of the successor then that will become the left node of successor parent.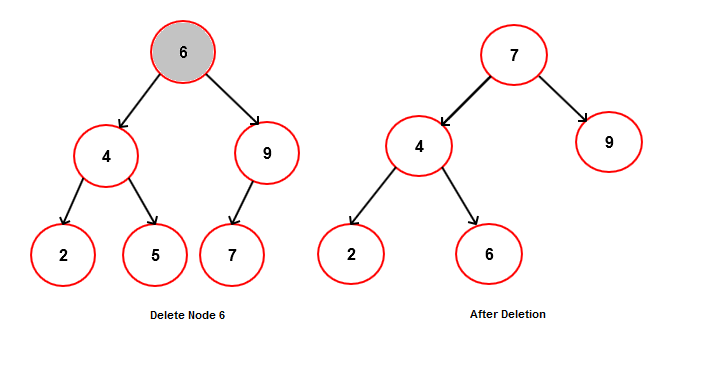

Please note that deletion can unbalanced the tree which can degrade the performance of most of the operations to O(n).

Java implementation to delete a node in Binary Search Tree

    public boolean deleteNode(int value) {
        Node curr = root;
        Node parent = root;
        boolean isLeftChild = false;
        // search for the node
        while (curr.value != value) {
            parent = curr;
            if (value < curr.value) {
                isLeftChild = true;
                curr = curr.left;
            }
            if (value > curr.value) {
                isLeftChild = false;
                curr = curr.right;
            }
            // if value is not in tree
            if (curr == null) {
                return false;
            }
        }
        // CASE-1: No child- point the deleted node parent to null.
        if (curr.left == null && curr.right == null) {
            if (curr == root) {
                root = null;
            } else if (isLeftChild) {
                parent.left = null;
            } else {
                parent.right = null;
            }
        }// CASE-2: One child- point the deleted node parent to the child of
         // deleted node.
        else if (curr.right == null) { // One child - left
            if (curr == root) {
                root = curr.left;
            } else if (isLeftChild) {
                parent.left = curr.left;
            } else {
                parent.right = curr.left;
            }
        } else if (curr.left == null) { // One child - right
            if (curr == root) {
                root = curr.right;
            } else if (isLeftChild) {
                parent.left = curr.right;
            } else {
                parent.right = curr.right;
            }
        } else {
            // CASE-3: Two Children- replace the node with its successor
            Node successor = getSuccessor(curr);

            if (successor != curr.right) {
                // If there is any right subtree of successor then point it to
                // the successor's parent left
                successor.parent.left = successor.right;
                // point right subtree of the deleted node to the right of
                // successor
                successor.right = curr.right;
            }

            if (curr == root) {
                root = successor;
            } else if (isLeftChild) {
                parent.left = successor;
            } else {
                parent.right = successor;
            }
            // point left subtree of the deleted node to the left of successor
            successor.left = curr.left;
        }
        return false;
    }

Go to the next page – Click on the below red circle with page number.