What is Dynamic programming?
- Dynamic programming was invented by a prominent U.S. mathematician, Richard Bellman, in the 1950s.
- Dynamic Programming is nothing to do with computer programming. Here programming means planning.
- It is a method for optimizing multistage decision making process.
- It is an algorithm design technique always considered to solve optimization problem.
- More efficient than “brute-force methods”, which solve the same subproblems over and over again.
When to use?
- Dynamic programming is used to solve problems which have overlapping sub-problems.
- When problem breaks down into recurring small dependent sub-problems.
- When the solution can be recursively described in terms of solutions to sub-problems.
How it works?
Dynamic programming algorithm finds solutions to sub-problems and stores them in memory for later use. It is sometimes considered the opposite of recursion. Where a recursive solution starts at the top and breaks the problem down, solving all small problems until the complete problem is solved, a dynamic programming solution starts at the bottom, solving small problems and combining them to form an overall solution to the big problem. It is used to convert algorithm of complexity 2n to O(n3) or O(n2).
It’s always better if you understand the Dynamic programming with the help of problems.
We will solve following problems with the help of Dynamic programming
- Fibonacci Series
- Coin Row Problem
- Change Making Problem
- Minimum Coin Change
- Robot Coin Collection
- Levenshtein distance
Let’s start with the easiest one Fibonacci series.
Fibonacci Series : As we know that Fibonacci series is the element of sequence
0,1,1,2,3,5,8,13,21,34,55. . . .
And nth Fibonacci number is defined by the recurrence relation
If n=0 then f(0) = 0
If n=1 then f(1) = 1
Otherwise f(n) = f(n-2)+f(n-1)
We can define a recursive method using this recurrence relation.
public int fibonacci_rec(int n) {
if (n <= 0) {
return 0;
}
if (n == 1) {
return 1;
}
return fibonacci_rec(n - 1) + fibonacci_rec(n - 2);
}
For example: suppose that we want to calculate 6th Fibonacci number using above method.
Recursion tree for 6th Fibonacci number
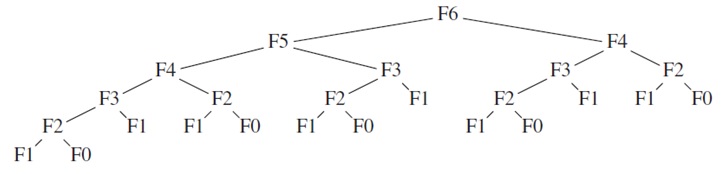
To compute F(6), there is one call to F(5) and F(4). However, since
F(5) recursively makes a call to F(4) and F(3), there are actually two separate calls
to compute F(4). If you will trace out the entire algorithm, you will observe that F(4) is computed two times, F(3) is computed three times, f(2) is computed five times, F(1) is computed eight times, and so on. We are re-computing the same values many times. The growth of redundant calculation is exponential.
We can improve it using Dynamic programming. We can use a single dimensional array as a cache to store the result of each computed Fibonacci number and before computing we will check in this array that if the value already exist. If exist then no need to recomputed.
public class FibonacciNumber {
private static final int MAXN = 45;
private Integer[] f = new Integer[MAXN];
public int fibonacci(int n) {
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= n; i++) { f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
}
Actually to calculate Nth Fibonacci we don’t need all the Fibonacci number from 1 to n-1, we just need previous two numbers ie (n-2) and (n-1).
public int fibonacci(int n) {
if(n==1){
return 0;
}
int back2 = 0;
int back1 = 1;
int next;
for (int i = 2; i < n; i++) {
next = back2 + back1;
back2 = back1;
back1 = next;
}
return back2 + back1;
}
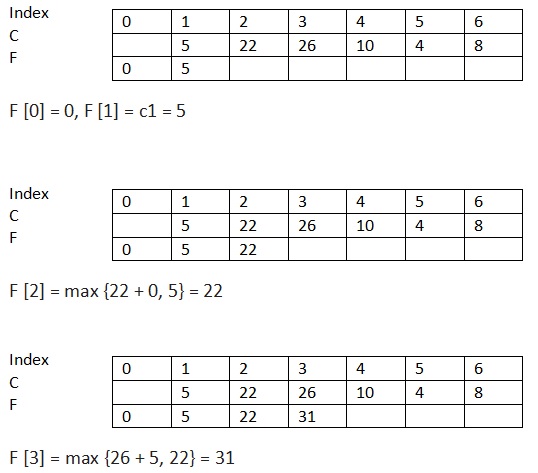
Coin Row Problem : Coin-rowproblem There is a row of n coins whose values are some positive integers c1, c2, . . . , cn, not necessarily distinct. The goal is to pick up the maximum amount of money subject to the constraint that no two coins adjacent in the initial row can be picked up.
Or in other words
There is an integer array consisting positive numbers only. Find maximum possible sum of elements such that there are no 2 consecutive elements present in the sum.
For ex: Coins[] = {5, 22, 26, 15, 4, 3,11}
Max Sum = 22 + 15 + 11 = 48
To solve this problem using Dynamic Programming first we will have to define recurrence relation.
Let F[n] is the array which will contain the maximum sum at n for any given n. The recurrence relation will be.
F(n) = max{Coins[n] + F[n − 2], F[n − 1]} for n > 1,
F(0) = 0, F(1) = Coins[1].
This is very easy to understand. While calculating F[n] we are taking maximum of coins[n]+the previous of preceding element and the previous element.
For example F[2] = max{coins[0]+ F[2-2], F[2-1]} // No consecutive
The algorithm:
public class CoinRow {
public static int getMaximumAmount(int[] coins) {
assert coins.length > 0 : "no coins to select";
int[] C = new int[coins.length + 1];
for (int i = 0; i < coins.length; i++) {
C[i + 1] = coins[i];// make room at first place
}
int[] F = new int[coins.length + 1];
F[0] = 0;
F[1] = C[1];
for (int i = 2; i <= coins.length; i++) {
F[i] = max(C[i] + F[i - 2], F[i - 1]);
}
return F[coins.length];
}
private static Integer max(int i, int j) {
return i > j ? i : j;
}
public static void main(String[] args) {
int[] coins = { 5, 22, 26, 10, 4, 8};
System.out.println(getMaximumAmount(coins));
}
}
Output
-------
40
F[6] will have the final value.
Go to the next page – Click on the below red circle with page number.