I would highly recommend to read below posts before getting into questions on stack and queue-
Questions On Stack and Queue
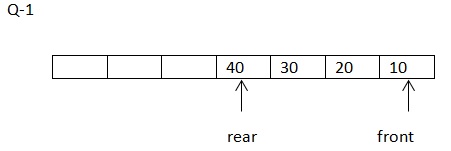
Problem-1: Show how to implement a queue using two stacks.
The difference between stack and queue is the order, stack uses last in first out(LIFO) and queue uses first in first out(FIFO). Our goal here is to convert LIFO to FIFO. To achieve FIFO using Stack somehow we will have to reverse the order of Stack. We can use our second Stack to reverse the order of the elements by popping from Stack-1 and pushing the elements on to Stack-2.
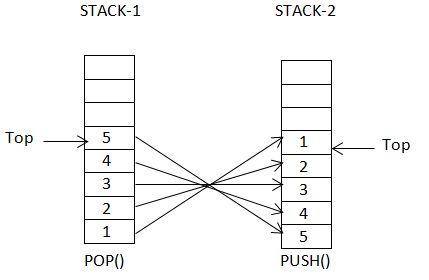
Stack-1 will thus be ordered with the newest elements on the top, while Stack-2 will have the oldest elements on the top. We push the new elements onto Stack-1, and peek and pop from Stack-2. When Stack-2 is empty, we’ll transfer all the elements from Stack-1 onto Stack-2, in reverse order.
public class QueueWithTwoStacks {
Stack oldStack;
Stack newStack;
public QueueWithTwoStacks() {
oldStack = new Stack();
newStack = new Stack();
}
public int size() {
return oldStack.size() + newStack.size();
}
public void enqueue(int value) {
newStack.push(value);
}
public int dequeue() {
shiftStack();
return oldStack.pop();
}
private void shiftStack() {
//shift only if old stack is empty
if (oldStack.size() == 0) {
while (newStack.size() > 0) {
oldStack.push(newStack.pop());
}
}
}
public static void main(String[] args) {
QueueWithTwoStacks queue = new QueueWithTwoStacks();
queue.enqueue(10);
queue.enqueue(18);
queue.enqueue(5);
queue.enqueue(29);
queue.enqueue(27);
queue.enqueue(6);
System.out.println(queue.dequeue());
System.out.println(queue.dequeue());
}
}
Output
--------
10
18
Problem-2: Show how to implement a Stack using two Queues.
This is just opposite of above question. Here we have to convert FIFO to LIFO and using two Queues. The solution is very simple.
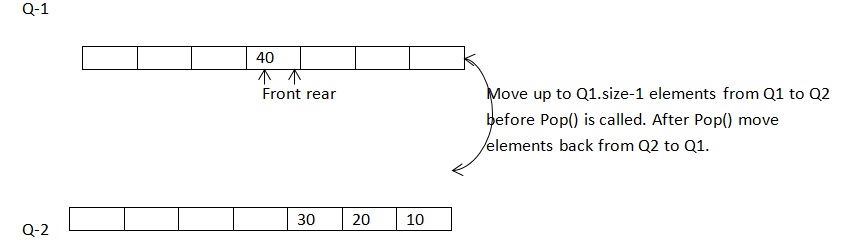
When Push() is called, enqueue() into Q1.
When Pop() is called, move up to Q1.size-1 elements from Q1 to Q2. Now Q1 has the last element, dequeue() this last element and move elements back from Q2 to Q1.
public class StackWithTwoQueues {
Queue oldQueue;
Queue newQueue;
public StackWithTwoQueues(){
oldQueue = new Queue();
newQueue = new Queue();
}
public void push(int item){
oldQueue.enqueue(item);
}
public Integer pop(){
copy(oldQueue,newQueue,1);//leave last element in old queue
int value =oldQueue.dequeue();//remove last element
copy(newQueue,oldQueue,0);//copy back all the elements
return value;
}
private void copy(Queue src,Queue target, int upto){
if(target.size()==0){
while(src.size()>upto){
target.enqueue(src.dequeue());
}
}
}
public static void main(String[] args) {
StackWithTwoQueues stack = new StackWithTwoQueues();
stack.push(50);
stack.push(10);
stack.push(4);
stack.push(34);
stack.push(3);
stack.push(12);
stack.push(60);
System.out.println(stack.pop());
System.out.println(stack.pop());
System.out.println(stack.pop());
stack.push(55);
stack.push(33);
System.out.println(stack.pop());
System.out.println(stack.pop());
System.out.println(stack.pop());
}
}
Output
---------
60
12
3
33
55
34
Problem-3: Design a stack which, in addition to push() and pop(), also has functions min() which returns minimum element and max() which return maximum element. All operations should operate in O(1) time.
Here we will decorate the original Stack by extending from it. The MinMaxStack will have two Stacks to maintain minimum and maximum values.
public class MinMaxStack extends Stack{
private Stack minStack;
private Stack maxStack;
public MinMaxStack(){
minStack = new Stack();
maxStack = new Stack();
}
public void push(int value){
if(min() ==-1 || value < min()){
minStack.push(value);
}
if(max() ==-1 || value > max()){
maxStack.push(value);
}
super.push(value);
}
public int pop(){
int value = super.pop();
if(value == min()){
minStack.pop();
}
if (value == max()) {
maxStack.pop();
}
return value;
}
public int min() {
if(minStack.size()>0){
return minStack.peek();
}
return -1;
}
public int max() {
if (maxStack.size() > 0) {
return maxStack.peek();
}
return -1;
}
public static void main(String[] args) {
MinMaxStack stack = new MinMaxStack();
stack.push(50);
stack.push(10);
stack.push(4);
stack.push(34);
stack.push(3);
stack.push(12);
stack.push(1);
System.out.println("MIN: "+stack.min());
System.out.println("MAX: "+stack.max());
}
}
Output
--------
MIN: 1
MAX: 50
Problem-4: Write a program to sort a stack in ascending order(with biggest item on top). You may use at most one additional stack to hold items, but you may not copy the elements into any other data structure.
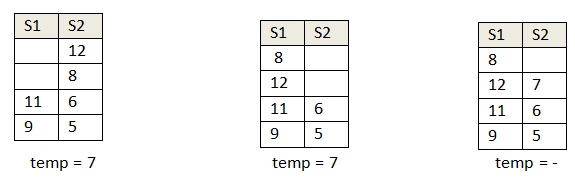
We have two stacks. Suppose that S2 is sorted and S1 is not sorted.
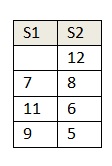
When we pop 7 from S1, it should be placed at the right position in S2 ie just above 6. We already have two elements 8 and 12 above 6. We can place 7 at right position in S2 by popping 7 from S1 and keeping it in a temporary variable. Then moving all the items from S2 to S1 which is greater than 7 and then push 7 to S2. Repeat the process for all the items in S1.
public class SortedStack {
public static Stack sortStack(Stack src){
Stack r = new Stack();
while(!src.isEmpty()){
int temp = src.pop();
while(!r.isEmpty() && r.peek() > temp){
src.push(r.pop());
}
r.push(temp);
}
return r;
}
public static void main(String[] args) {
Stack s = new Stack();
s.push(10);
s.push(12);
s.push(8);
s.push(7);
s.push(11);
s.push(5);
Stack r =SortedStack.sortStack(s);
for(int i=0;i<6;i++){
System.out.print(r.pop()+" ");
}
}
}
Output
----------
12 11 10 8 7 5
References:
- Cracking The Coding Interview- Gayle Laakmann McDowell
- Programming Interviews Exposed- John Mongan, Eric Giguère, Noah Kindler.
- Coding Interviews- Harry He